파이썬을 활용한 금융분석 - 이브 힐피시 책 내용을 기반으로 colab, jupyter notebook 으로 직접 코드 구현해보며 공부한 내용이다.
매매 전략 구현
알고리즘을 기반으로 매수, 매도, 중립 등 포지션을 취하도록 설계된 모든 종류의 금융 매매 전략을 구현해본다.
(또한 과거 데이터로 분류 알고리즘을 학습시켜 미래 시장 방향을 예측하고자 하는 목표도 있다.
-> 실수로 된 금융 데이터를 소수의 범주형 값으로 변환해야함)
1. 단순 이동평균
2. 랜덤워크 가설 : 시장 가격이 무작위한 움직임을 따른다는 가설.
3. 선형 회귀분석
4. 클러스터링 : 비지도 학습
5. 빈도주의 방법론
6. 분류 알고리즘
7. 심층 신경망
단순 이동 평균
import numpy as np
import pandas as pd
import datetime as dt
from pylab import mpl,plt
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
#데이터 읽기
raw = pd.read_csv('https://hilpisch.com/tr_eikon_eod_data.csv',
index_col=0, parse_dates=True)
raw.info()
#애플 주식 선택 (일간 데이터 기반)
symbol = 'AAPL.O'
data = (
pd.DataFrame(raw[symbol]).dropna()
)
#기간을 다르게 선택하여 단순이동평균 계산
SMA1 = 42
SMA2 = 252
data['SMA1'] = data[symbol].rolling(SMA1).mean()
data['SMA2'] = data[symbol].rolling(SMA2).mean()
data.plot(figsize=(10, 6))
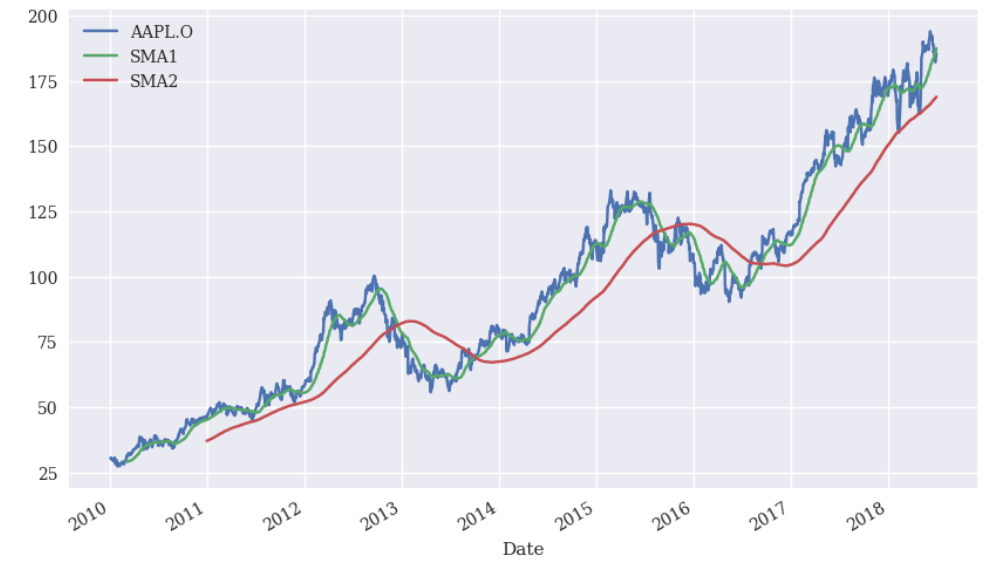
이후에 잔고포지션을 계산하여 매매규칙을 세운다.
1. 단기 이동평균선이 장기 이동평균선 위에 있으면 매수 (+1)
2. 장기 이동평균선이 단기 이동평균선 위에 있으면 매도 (-1)
data.dropna(inplace = True)
# np.where(cond, a, b) : 조건이 되는 원소 cond 값이 True면 a, False면 b 출력
data['Position'] = np.where(data['SMA1'] > data['SMA2'], 1, -1)
ax = data.plot(secondary_y = 'Position', figsize = (10,6))
ax.get_legend().set_bbox_to_anchor((0.25, 0.85))

다음으로 벡터화된 백테스팅 진행. (특정 전략, 알고리즘을 사용해 과거 데이터에 대해 거래를 시뮬레이션해 해당 전략 성능을 평가하는 프로세스)
1. 로그 수익률 계산
2. +1, -1로 나타낸 포지션을 수익률에 곱한다. (수익률이 양수인 기간은 매수 수익, 수익률이 음수인 구간은 매도수익)
3. 원래 애플 주가와 알고리즘 트레이딩 수익률을 모두 더한 후 지수함수를 적용해 최종 성과 계산.
data['Returns'] = np.log(data[symbol] / data[symbol].shift(1)) #애플 주가 로그 수익률 계산
data['Strategy'] = data['Position'].shift(1) * data['Returns'] #포지션 값을 하루 늦추고 로그 수익률을 곱함(미래 예측을 막기 위함)
data.round(4).head()
data.dropna(inplace = True)
np.exp(data[['Returns', 'Strategy']].sum()) #로그 수익률의 합을 계산한 후 지수함수를 적용해 절대 성과 게산
data[['Returns', 'Strategy']].std() * 252 ** 0.5 #전략과 벤치마크 투자 연율화된 변동성 계산
성과를 시각화 하기 위해 애플 주식과 알고리즘 트레이딩 전략의 성과를 시간 경과에 따라 그래프화 해본다.
ax = data[['Returns' , 'Strategy']].cumsum().apply(np.exp).plot(figsize = (10,6))
data['Position'].plot(ax = ax, secondary_y = 'Position' , style = '--')
ax.get_legend().set_bbox_to_anchor((0.25, 0.85));

이후 SMA1과 SMA2에 대한 여러 값 조합을 통해 가장 좋은 수익률을 찾아내는 최적화 과정을 진행한다.
from itertools import product
import pandas as pd
import numpy as np
sma1 = range(20, 61, 4) #SMA1 매개변수 설정
sma2 = range(180, 281, 10) #SMA2 매개변수 설정
results = pd.DataFrame()
for SMA1, SMA2 in product(sma1, sma2): #SMA1 매개변수와 SMA2 매개변수 조합
data = pd.DataFrame(raw[symbol])
data.dropna(inplace=True)
data['Returns'] = np.log(data[symbol] / data[symbol].shift(1))
data['SMA1'] = data[symbol].rolling(SMA1).mean()
data['SMA2'] = data[symbol].rolling(SMA2).mean()
data.dropna(inplace=True)
data['Position'] = np.where(data['SMA1'] > data['SMA2'], 1, -1)
data['Strategy'] = data['Position'].shift(1) * data['Returns']
data.dropna(inplace=True)
perf = np.exp(data[['Returns', 'Strategy']].sum())
#모든 벡터화된 백테스팅 결과를 DataFrame 객체에 저장
results = pd.concat([results, pd.DataFrame(
{'SMA1': SMA1, 'SMA2': SMA2,
'MARKET': perf['Returns'],
'STRATEGY': perf['Strategy'],
'OUT': perf['Strategy'] - perf['Returns']},
index=[0])], ignore_index=True)
results.info()
results.sort_values('OUT', ascending=False).head(7)

벡테스팅 중 성능이 좋은 7개 매개변수 조합을 출력 해 볼 수 있다.
성능에 대한 순위는 알고리즘 트레이딩 전략이 벤치마크 투자를 앞선 정도를 바탕으로 매겨졌다(OUT 컬럼 내림차순)
벤치마크 투자 성과가 달라지는 이유는 SMA2 매개변수에 따라 전체 투자 기간과 백테스팅에 사용되는 데이터가 달라지기 때문이다.
이 방법은 사용된 데이터에 심하게 의존하므로 과최적화 되어있을 수 있으니 학습용 데이터를 사용해 최적화하고 검증용 데이터를 사용해 검사하는 방법을 추천한다.
(과최적화 : 매개변수가 학습에 사용된 데이터에만 최적화되고 실제로 사용할 다른 데이터에 대해서는 최적화되지 않은 것을 의미)
선형 회귀 분석
과거 로그 수익률을 기반으로 시장 방향성을 예측하는데 선형 회귀분석을 적용해본다.
두 가지 특징값을 사용
1. 시계열상 하루 전 로그 수익률
2. 이틀 전 로그 수익률
로그 수익률은 가격과 달리 정상 상태이므로 통계, 머신러닝 알고리즘을 적용할 수 있다.
지연 수익률을 사용하는 기본 아이디어는 과거 수익률로 미래 수익률을 예측 할 수 있다는 점에 기반한다.
ex) 이틀 연속 하락하면 다음 날은 상승 (평균 회귀 패턴)
ex) 반대로 계속 하락하는 (모멘텀 혹은 추세) 패턴 유지
먼저 환율의 로그 수익률 데이터를 시각화해본다.
symbol = 'EUR='
data = pd.DataFrame(raw[symbol])
data['returns'] = np.log(data / data.shift(1))
data.dropna(inplace = True)
data['direction'] = np.sign(data['returns']).astype(int)
data.head()
data['returns'].hist(bins = 35, figsize = (10,6))
다음으로 로그 수익률을 지연시켜 특징 데이터를 생성
(시각화 그래프에서는 원래 수익률 데이터와 함께 확인할 수 있다.)
lags = 2
def create_lags(data) :
global cols
cols = []
for lag in range(1, lags + 1):
col = 'lag_{}'.format(lag)
data[col] = data['returns'].shift(lag)
cols.append(col)
create_lags(data)
data.head()
data.dropna(inplace=True)
data.plot.scatter(x='lag_1', y='lag_2', c='returns', cmap='coolwarm', figsize=(10,6), colorbar=True)
plt.axvline(0, c='r', ls='--')
plt.axhline(0, c='r', ls='--')

* 회귀분석
데이터 준비 후 선형 회귀분석을 적용해 데이터 간 잠재적 선형관계를 학습하고, 특징 값에 기반해 시장 움직임을 예측한다. 이후 예측값을 사용해 매매 전략을 백테스팅한다.
이때 로그 수익률을 종속변수로 사용하거나 로그 수익률의 방향을 종속변수로 사용할 수 있다.
예측 결과인 방향을 +1, -1 숫자로 바꿔 어떤 경우든 예측 결과의 형식은 달라지지 않도록 한다.
#사이킷런 선형 회귀분석 기능 사용
from sklearn.linear_model import LinearRegression
model = LinearRegression()
#로그 수익률을 직접 사용해 회귀분석
data['pos_ols_1'] = model.fit(data[cols], data['returns']).predict(data[cols])
#로그 수익률 방향을 사용해 회귀분석
data['pos_ols_2'] = model.fit(data[cols], data['direction']).predict(data[cols])
data[['pos_ols_1', 'pos_ols_2']].head()
#실숫값을 +1, -1로 변환
data[['pos_ols_1', 'pos_ols_2']] = np.where(data[['pos_ols_1', 'pos_ols_2']] > 0, 1, -1)
#두 방법론이 다른 방향을 가리킴
data['pos_ols_1'].value_counts() #-1 1847, 1 288
data['pos_ols_2'].value_counts() #1 1377, -1 758
# 두 방법 모두 다수의 매매로 이어짐을 볼 수 있음
(data['pos_ols_1'].diff() != 0).sum() #555
(data['pos_ols_2'].diff() != 0).sum() #762
방향을 예측하는 벡터화된 백테스팅을 적용해 매매 전략의 성과를 판단할 수 있다.
이 단계에서는 분석을 할 때 두 가지 단순화 가정을 한다.
1. 거래 비용이 들지 않는다는 것
2. 학습 및 검증에 같은 데이터를 사용한다는 것
#첫번째 전략 수익률 계산
data['strat_ols_1'] = data['pos_ols_1'] * data['returns']
#두번째 전략 수익률 계산
data['strat_ols_2'] = data['pos_ols_2'] * data['returns']
#각 전략과 시장 수익률의 누적 수익률 계산
data[['returns', 'strat_ols_1', 'strat_ols_2']].sum().apply(np.exp)
#첫번째 전략 예측 포지션-실제 포지션 일치 여부 확인
(data['direction'] == data['pos_ols_1']).value_counts()
#두번째 전략 예측 포지션-실제 포지션 일치 여부 확인
(data['direction'] == data['pos_ols_2']).value_counts()
#각 전략과 시장의 누적 수익률 계산 시각화 진행
data[['returns', 'strat_ols_1', 'strat_ols_2']].cumsum().apply(np.exp).plot(figsize = (10,6))
위 가정하에 회귀 분석을 기반으로 한 두 전략의 성과는 패시브 벤치마크 투자의 성과보다 높다는 결과를 보여주고, 방향을 학습한 전략은 평균적으로 양의 수익률을 보이는 그래프 결과를 도출할 수 있다.
클러스터링
다음으로는 k-means 클러스터링을 시계열 데이터에 적용해 매매 전략을 수립하는데 사용할 클러스터를 만드는 실습을 진행한다.
시장의 움직임을 예측할 수 있는 특징값의 클러스터를 식별하기 위함이다.
from sklearn.cluster import KMeans
#두 개의 클러스터로 구성된 KMeans 모델 생성
model = KMeans(n_clusters=2, random_state = 0)
#데이터 특성 cols 에 대해 학습 진행
model.fit(data[cols])
#각 데이터 포인트를 예측된 클러스터에 할당
data['pos_clus'] = model.predict(data[cols])
#클러스터 번호가 1인 경우 매도(-1), 그렇지 않은 경우 매수(1) 포지션 할당
data['pos_clus'] = np.where(data['pos_clus'] == 1, -1, 1)
#클러스터 결과를 포함한 포지션 배열 반환
data['pos_clus'].values
plt.figure(figsize=(10, 6))
#산점도 시각화 진행
#각각의 데이터 포인트는 cols 첫번째 두번째 특성에 대한 위치에 표시
plt.scatter(data[cols].iloc[:, 0], data[cols].iloc[:, 1], c=data['pos_clus'], cmap='coolwarm')

해당 방법은 실습코드를 위함으로 임의적이므로 실제에는 사용하기 어렵다.
(비지도 학습으로 올바른 예측을 나타내는 hit ratio 값이 50%도 되지 않음 주의)
data['strat_clus'] = data['pos_clus'] * data['returns']
data[['returns' , 'strat_clus']].sum().apply(np.exp)
(data['direction'] == data['pos_clus']).value_counts()
data[['returns', 'strat_clus']].cumsum().apply(np.exp).plot(figsize = (10,6))
분류 알고리즘
로지스틱 회귀, 가우스 나이브 베이즈, 서포트 벡터 머신 방법등을 적용해본다.
이진수 특징값에 기반해 모델을 학습시키고 결과로 나온 포지션 정보를 받는 예제 소스를 작성한다.
먼저 데이터를 이산화하고, 그룹화하여 통계 계산, 시각화 분석 프로세스를 먼저 진행한다.
#데이터에 이산화된 열을 생성하는 함수 정의
def create_bins(data, bins=[0]):
#이후에 접근할 수 있도록 전역변수 cols_bin을 선언
global cols_bin
cols_bin = [] #이산화된 열 이름 저장 리스트 초기화
for col in cols: #주어진 열에 대해 반복문 실행
col_bin = col + '_bin' #이산화된 열의 이름 설정
#주어진 구간으로 데이터 이산화하여 새로운 열 생성
data[col_bin] = np.digitize(data[col], bins=bins)
cols_bin.append(col_bin) #생성된 이산화된 열 이름 리스트에 추가
# 함수 호출, 이산화된 열 생성
create_bins(data)
# 이산화된 열과 'direction' 열 기준으로 데이터 그룹화
grouped = data.groupby(cols_bin + ['direction'])
#각 그룹별로 'direction' 열 크기를 계산해 피벗테이블로 변환
res = grouped['direction'].size().unstack(fill_value=0)
# 'cols_bin'에 대해 각 행의 합이 2인 경우 매도 (-1), 그렇지 않은 경우 매수 (1) 포지션 할당
data['pos_freq'] = np.where(data[cols_bin].sum(axis = 1) == 2, -1, 1)
#실제 포지션과 'pos_freq' 포지션의 일치 여부를 확인하고 값 카운트
(data['direction'] == data['pos_freq']).value_counts()
# 'pos_freq' 포지션에 기반해 전략 평가
data['strat_freq'] = data['pos_freq'] * data['returns']
#전략 및 시장 수익률 누적 수익률 계산
data[['returns' , 'strat_freq']].sum().apply(np.exp)
#전략 및 시장 누적 수익률 계산해 시각화 진행
data[['returns', 'strat_freq']].cumsum().apply(np.exp).plot(figsize = (10, 6))
다음으로 두 개의 이진수 특징값에 기반해 모델을 학습시키고 결과로 나온 포지션 정보를 받는다.
학습 결과로 나온 매매 전략에 벡터화된 백테스팅을 적용하여 시각화를 진행한다.
from sklearn import linear_model
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
#정규화 파라미터
C=1
#모델 정의
models = {
'log_reg' : linear_model.LogisticRegression(C=C), #로지스틱 회귀 모델
'gauss_nb' : GaussianNB(), # 가우시안 나이브베이즈 모델
'svm' : SVC(C=C) #서포트 벡터 머신 모델
}
#모델 학습 함수 정의
def fit_models(data) :
#각 모델을 학습하고 모델 객체를 mfit 딕셔너리 저장
mfit = {model : models[model].fit(data[cols_bin] , data['direction'])
for model in models.keys()}
#모델학습
fit_models(data)
# 모델을 사용해 위치를 파생하는 함수 정의
def derive_positions(data) :
for model in models.keys():
#각 모델을 사용해 데이터 위치를 파생하고 'pos_'+ 모델명으로 열 추가
data['pos_' + model] = models[model].predict(data[cols_bin])
#각 모델로부터 위치 파생
derive_positions(data)
#전략을 평가하는 함수 정의
def evaluate_strats(data):
global sel
sel = []
for model in models.keys():
col = 'strat_' + model
# 각 모델을 사용해 수익률 계산 'strat_' 모델명으로 열 추가
data[col] = data['pos_' + model] * data['returns']
sel.append(col)
sel.insert(0, 'returns') # 'returns' 열을 첫 번째로 추가
#각 모델의 전략 평가
evaluate_strats(data)
sel.insert(1, 'strat_freq')
data[sel].sum().apply(np.exp)
#각 전략 및 시장 누적수익률을 계산해 출력
data[sel].cumsum().apply(np.exp).plot(figsize = (10,6))

다음으로 전략 성능을 향상시키기 위해 이진수 특징값을 두 개가 아니라 다섯 개 사용한다.
data = pd.DataFrame(raw[symbol])
data['returns'] = np.log(data / data.shift(1))
data['direction'] = np.sign(data['returns'])
lags = 5
create_lags(data)
data.dropna(inplace = True)
create_bins(data)
data.dropna(inplace = True)
fit_models(data)
derive_positions(data)
evaluate_strats(data)
data[sel].sum().apply(np.exp)
data[sel].cumsum().apply(np.exp).plot(figsize = (10,6))
결과를 보면 서포트 벡터 기반 전략 성능은 향상되었으나, 로지스틱 회귀와 가우스 나이브 베이즈 기반 전략의 성능은 떨어졌음을 볼 수 있다.
'스터디 > Tech' 카테고리의 다른 글
| [Tech] Process Control Optimization 공정 제어 최적화 (1) | 2024.12.18 |
|---|---|
| [Python] 디자인 패턴(Design Patterns) (0) | 2024.12.16 |
| [기술서적] 파이썬을 활용한 금융 분석 - 통계분석 중 머신러닝 (3) | 2024.03.12 |
| [기술서적] 파이썬을 활용한 금융 분석 - 확률 과정 (0) | 2024.03.10 |
| [기술서적] 파이썬을 활용한 금융 분석 - 수학용 도구 (1) | 2024.03.03 |