Udemy 강의 중 비즈니스 데이터 사이언스 사례 강의를 들으며 공부한 내용을 정리한 글이다.
연구 목표 설정
기본적인 목표 : 고객 시장 세분화를 위해 타겟이 되는 고객을 정한다.
은행 고객 데이터를 통해 타겟 마케팅 광고 캠페인을 진행한다.
사용 데이터 특성 : 회원 아이디 / 잔고 / 잔고 업데이트 빈도 / 구매에 사용되는 금액 / 할부 결제 양 / 현금 서비스 이용 수 / 일시불 구매 빈도 / 할부 금액 빈도 등
라이브러리 & 데이터 집합 가져오기
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, normalize
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
#데이터 구글 드라이브에 마운트
from google.colab import drive
drive.mount('/경로')
#데이터 가져오기
creditcard_df = pd.read_csv('/데이터경로')
#데이터 확인
creditcard_df
#데이터 파악
creditcard_df.info()
creditcard_df.describe()
#특정 데이터 확인해보기 : 일시불로 4만달러 쓴 사람 누구인지 확인
creditcard_df[craditcard_df['ONEOFF_PURCHASES'] == 40761.250000 ] #특정 열만 추출됨
#특정 데이터 확인해보기 : 현금 서비스 이용금액이 가장 높은 사람 확인
creditcard_df['CASH_ADVANCE'].max() #현금 서비스 가장 높은 금액 확인, 47137.21176
creditcard_df[craditcard_df['CASH_ADVANCE'] == 47137.21176 ] #특정 열만 추출됨
데이터 세트 탐색 & 시각
결측치를 확인한다.
#히트맵으로 결측치확인
sns.heatmap(creditcard_df.isnull(), yticklabels = False, cbar = False, cmap = 'Blues')
creditcard_df.isnull().sum() #결측치 항목 개수 도출
평균값으로 결측치를 채운다.
creditcard_df.loc[(creditcard_df['MINIMUM_PAYMENTS'].isnull() == True), 'MINIMUM_PAYMENTS'] = creditcard_df['MINIMUM_PAYMENTS'].mean()
#결측치가 채워졌는지 확인
creditcard_df.isnull().sum()
필요없는 ID 컬럼 삭제
#먼저 중복 행 있는지 확인
creditcard_df.duplicated().sum() #0으로 없음
#ID 컬럼 삭제
creditcard_df.drop['CUST_ID', axis = 1, inplace = True)
다음으로 KDE와 히스토그램을 합친 distplot을 이용해 시각화를 진행한다.
(seaborn 중 distribution을 표현, seaborn 공홈에서 안내하 v0.14.0 에서 제거될 예정으로 histplot()으로 대체된다고 한다.)
plt.figure(figsize = (10, 50))
#반복문을 통해 각 컬럼별 시각화진행
for i in range(len(creditcard_df.columns)):
plt.subplot(17, 1, i+1)
sns.distplot(creditcard_df[creditcard_df.columns[i]], kde_kws = {'color' : 'b', 'lw' : 3, 'label' : 'KDE'} , hist_kws = {'color' : 'g'})
plt.title(creditcard_df.columns[i])
plt.tight_layout()

간단히 그래프를 살펴보면 잔고는 대부분 고객이 1500 달러 정도를 지녔음을 볼 수 있다.
구매 빈도는 1에 가깝기 때문에 대부분 신용카드를 자주 쓴다는 것을 알 수 있다. (잔고 업데이트가 빈번)
평균 구매 금액은 1000달러 정도된다.

구매 빈도는 양극화 되어있음을 볼 수 있는데 신용카드를 자주 이용하지 않는 고객 / 신용카드를 자주 이용하는 고객이 명확히 나뉨을 알 수 있다. (군집을 다룰 때 유용할 수 있다)
다음으로 히트맵을 통해 특성간 상관관계 시각화를 진행한다.
f, ax = plt.subplots(figsize = (20, 20))
sns.heatmap(correlations, annot = True)
K-means 알고리즘
k-means(k평균) 알고리즘은 비지도 학습에 속하며 비슷하게 위치한 데이터를 그룹으로 묶어 군집화한다.
즉 알고리즘이 데이터를 비교해 유클리드 거리값이 비슷한 데이터들끼리 묶어준다.
알고리즘 단계
1. 군집 수 k를 정한다
2. 각 군집의 중심이 될 랜덤 k 포인트 지정
3. 랜덤 포인트 중심의 군집 생성 (k개)
4. 각 군집의 새로운 중심을 계산
5. 각각 데이터들을 새로운 중심 기준으로 재 그룹핑 진행
(4-5-6 반복)
최적의 k를 구하는 방법으로는 'elbow method'가 있다.
군집 내 제곱의 합을 구해야함(WCSS).
각 데이터 좌표들과 중심점의 거리를 계산하고 각 Pi(군집)들 끼리의 거리도 계산한다.
군집 수가 적을수록 군집 내 거리 제곱 합은 커지고, 군집 수를 늘려가면서 거리 제곱 합은 점차 줄어들게 된다.
이런식으로 군집 내 제곱 합을 y, 군집의 수를 x로 그래프를 그리면
군집 수 x가 점점 늘어날수록 군집 내 제곱합 y가 낮아지는 그래프가 된다.

이런식으로 최적의 k 값을 얻어내는데, k의 변화가 미미해지는 시작점을 팔꿈치(elbow)라고 지칭하며 해당 부분이 최적의 k 값이라고 판명한다.
아래는 k-means 알고리즘에 대한 실습코드이다.
#표준 스케일링 진행
scaler = StandardScaler()
creditcard_df_scaled = scaler.fit_transform(creditcard_df)
elbow 메소드 적용
scores_1 = [] #모든 값 누적
range_values = range(1, 20)
for i in range_values : # k평균 알고리즘 20번 반복
kmeans = KMeans(n_clusters = i)
kmeans.fit(creditcard_df_scaled)
scores_1.append(kmeans.inertia_) #inertia_는 군집 내 제곱합(WCSS)의미
plt.plot(scores_1, 'bx-')
plt.title('Finding the right number of clusters')
plt.xlabel('Clusters')
plt.ylabel('WCSS')
plt.show()
7~8개일때부터 변화가 미미함을 볼 수 있다. 따라서 군집 k 수를 7, 8, 9 정도로 잡고 알고리즘 step을 시작하면 된다.
K-means 알고리즘을 적용해 시장세분화 해보기
먼저 각 데이터 행마다 속하는 군집이 무엇인지 표시하는 열을 추가해준다.
creditcard_df_cluster = pd.concat([creditcard_df, pd.DataFrame({'Cluster' : labels})], axis = 1)
#열이 추가되었는지 확인
creditcard_df_cluster.head()
다음으로 군집들을 히스토그램으로 시각화한다.
for i in creditcard_df.columns :
plt.figure(figsize = (35, ,5))
for j in range(8): #군집 내 모든값까지 반복
plt.subplot(1, 8, j+1)
cluster = creditcard_df_cluster[ creditcard_df_cluster['cluster'] == j ]
cluster[i].hist(bins = 20)
plt.title('{} \nCluster {}'.format(i, j))
plt.show()

주성분 분석(PCA)
비지도 머신 러닝 알고리즘으로 차원 축소를 수행하기 위해 주로 사용한다.
특성을 줄일 때 정보를 최대한 잃지 않은 채, 차원만 줄이도록 하기 위함.
주성분 분석을 통한 차원축소는 원 데이터의 정보를 최대한 포함한 채 이루어지고, 특성들을 다시 성분으로 만드는 방식으로 진행된다.
+ 사용되는 input 데이터가 독립변수라 상관관계가 없다면 차원축소를 수행하기 힘들다는 특징이 있음.
다음은 주성분 분석을 시행하고 시각화해보는 예제이다.
#sklearn 사용, 2개의 성분으로 압축
pca = PCA(n_components = 2)
principal_comp = pca.fit_transform(credictcard_df_scaled)
#데이터 확인, 성분 수가 2기 때문에 모든 데이터가 2열이 됨
principal_comp
#데이터 프레임으로 변환
pca_df = pd.DataFrame(data = principal_comp, columns = ['pca1' , 'pca2'])
pca_df.head() #데이터 확인
#데이터 합치기
pca_df = pd.concat([pca_df, pd.DataFrame({'cluster' : labels})], axis = 1)
pca_df.head()
#데이터 시각화
plt.figure(figsize = (10,10))
ax = sns.scatterplot(x = 'pca1' , y = 'pca2', hue = 'cluster', data = pca_df, palette = ['red', 'green', 'blue', 'pink', 'yellow' , 'gray', 'purple', 'black'])
plt.show()

오토인코더
인공신경망, 정보처리 모델은 뉴런을 수학적으로 연결시켜 인풋, 아웃풋 데이터를 연결한다.
분류, 회귀, 이미지 인식, 물체 탐지 등에 사용되고 있다.
오토인코더는 인공신경망의 일종으로 데이터 인코딩 작업을 수행하기 위해 사용된다.
인코더 + 디코더 네트워크가 반전되어 연결된 구조이다.
인코더가 작동하는 원리를 보면
은닉층과 코드층이 있는데 데이터가 은닉층을 통해 차원을 축소하고 압축하며 정보가 소실되지 않도록 한다.
그리고 코드 층에 다다르면 데이터 업샘플링을 통해 이미지를 동일하게 재구성해낸다.
(주성분 분석과 마찬가지로 상관관계가 없는 데이터는 잘 동작하지 않음)
인코더가 잘 작동했다면
input 데이터로 들어간 x 값과 최종 도출되는 x햇 값이 축소됨 없이 매우 비슷하게 도출된다.
또한 인풋-은닉층 사이의 가중치 W와 은닉층-아웃풋 사이의 가중치 W*가 동일한 값을 가진다.
(tied weights = tied 가중치라고 불림)
다음은 오토인코더를 통해 차원축소를 진행하는 실습 코드이다.
#오토인코더를 통해 차원축소 수행
#Keras api 사용
from tensorflow.keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, Dropout
from tensorflow.keras.models import Model, load_model
from tensorflow.keras.initializers import glorot_uniform
from keras.optimizers import SGD
#네트워크 빌드
input_df = Input(shape = (17,))
x = Dense(7, activation = 'relu')(input_df)
x = Dense(500, activation = 'relu', kernel_initializer='glorot_uniform')(x)
x = Dense(500, activation = 'relu', kernel_initializer='glorot_uniform')(x)
x = Dense(2000, activation = 'relu', kernel_initializer='glorot_uniform')(x)
#인코더
encoded = Dense(10, activation = 'relu', kernel_initializer='glorot_uniform')(x)
x = Dense(2000, activation = 'relu', kernel_initializer='glorot_uniform')(encoded)
#디코더
decoded = Dense(17, activation = 'relu', kernel_initializer='glorot_uniform')(x)
#오토인코더 코드 작성
autoencoder = Model(input_df, decoded)
#전체 인코더 네트워크 작성
encoder = Model(input_df, encoded)
autoencoder.compile(optimizer = 'adam', loss = 'mean_squared_error')
오토인코더 네트워크를 만든 후 실제로 fit 을 통해 학습시켜본다.
autoencoder.fit(creditcard_df_scaled, creditcard_df_scaled, batch_size = 128, epochs = 25, verbose= 1)
fit을 실행하면 각각 에포크가 진행된다.
fit이 완료되면 오토인코더의 실제 구조를 확인해본다.
autoencoder.summary()
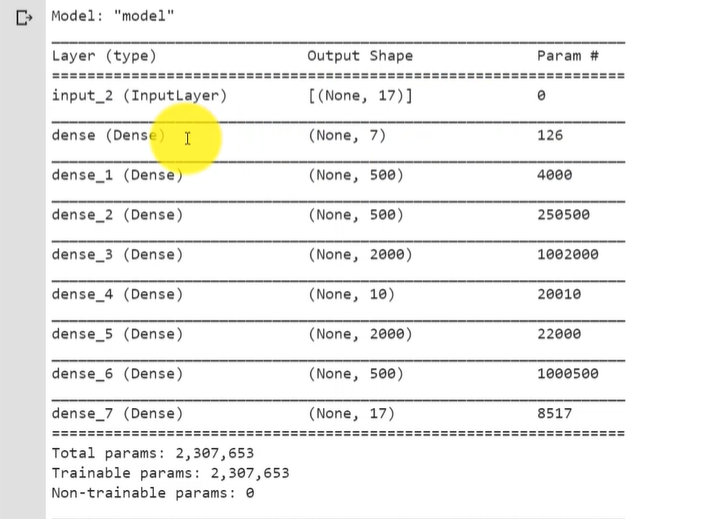
summary() 결과 오토인코더에 약 2천3백만개의 파라미터가 있음을 확인할 수 있다.
인코딩 차원의 수는 7, 각 Dense 층에 아웃풋 Param도 확인할 수 있다.
(마지막 아웃풋은 17)
주목할 점은 입력층과 출력층은 동일한 차원의 수를 가진다는 점!
중간에 네트워크에 병목을 만들어(dense_4) 인코더 네트워크에서 출력된 값을 받아 특성이 줄어듦을 볼 수 있다.
다음으로 k-means를 이용해 차원을 축소하는 실습코드이다.
먼저 데이터를 확인해둔다.
pred = encoder.predict(creditcard_df_scaled)
pred.shape #데이터 확인, (8950, 10)결과로 특성이 기존 17개에서 10개로 줄어듦을 볼 수 있다.
먼저 최적의 군집 수를 확인하고, k-means 알고리즘과 주성분 분석을 적용해 결과를 시각화해본다. (오토인코더를 통해 나온 10개 특성 사용)
#새로운 벡터값 생성
scores_2 = []
range_values = range(1, 20)
for i in range_values: #모든 군집 수에 k-means 적용
kmeans = KMeans(n_clusters = i)
kmeans.fit(pred)
scores_2.append(kmeans.inertia_) #kmeans.inertia_ 군집 내 제곱합 의미
plt.plot(scores_2, 'bx-')
plt.title('Finding right number of clusters')
plt.xlabel('Clusters')
plt.ylabel('scores')
plt.show()
이제 앞서 만들어보았던 scores_1 값과 scores_2 값을 시각화를 통해 비교해본다.
plt.plot(scores_1, 'bx-', color = 'r')
plt.plot(scores_2, 'bx-', color = 'g')
scores_1은 군집 8개를 이용했었고, scores_2는 수치 하락 폭이 처음엔 컸으나 다음엔 조금 줄고 그 후는 큰 차이가 없음을 볼 수 있다.
값의 변화가 줄어드는 시작점을 4, 5 정도로 정하면 적당할 듯 싶다.
kmeans = KMeans(4)
kmeans.fit(pred)
labels = kmeans.labels_
#데이터 프레임에 cluster 컬럼 추가
df_cluster_dr = pd.concat([creditcard_df, pd.DataFrame({'cluster' : labels})], axis = 1)
df_cluster_dr.head()
다음은 주성분 분석을 적용한다.
pca = PCA(n_components = 2)
prin_comp = pca.fit_transform(pred)
pca_df = pd.DataFrame(data = prin_comp, columns = ['pca1', 'pca2'])
#레이블을 데이터프레임에 추가
pca_df = pd.concat([pca_df, pd.DataFrame({'cluster' : labels})], axis = 1)
pca_df.head() #데이터 확인
plt.figure(figsize = (10, 10))
#네가지 군집을 위해 네가지 색상을 사용해서 스캐터플롯 시각화 진행
ax = sns.scatterplot(x = 'pca1', y = 'pca2', hue = 'cluster', data = pca_df, palette = ['red', 'green', 'blue', 'yellow'])
실습코드를 간단히 요약하자면,
처음 17개 특성으로 시작해 오토인코더를 통해 10개 특성으로 줄인 후
주성분 분석을 적용해 최종적으로 2개의 성분으로 만들고 4개의 군집으로 스캐터 플롯 시각화를 진행하였다.
'스터디 > Data' 카테고리의 다른 글
| [Imple] 비즈니스 사례 실습 : 영업(Sales department) 사례 (1) | 2024.04.12 |
|---|---|
| [Imple] 비즈니스 사례 실습 : 인사팀(personnel management) 사례 (0) | 2024.03.19 |
| [Imple] 데이터 프레임 (0) | 2024.02.18 |
| [Imple] 데이터 핸들링을 위한 Pandas (3) | 2024.02.13 |
| [이론] 데이터 분석 간단 통계학 (0) | 2024.01.30 |